Durchschnitt der Endpunkte einer linearen Trendlinie, genutzt um eine Prognose der Kursbewegungen zu erstellen
Die Lineare Regression, auch genannt Linear Regression, Gleitender linearer Regressionsindikator oder Zeitserien-Voraussage, stellt die Werte von Endpunkten vormaliger linearer Regressionstrendlinien über eine definierte Periode dar. Dazu wird mithilfe der Methode der kleinsten Quadrate aus der Punktwolke eine Haupttrendlinie ermittelt. Diese Regressionsgerade folgt dem Trend des Kursverlaufs eng und gibt die Trendrichtung so genauestens wieder.
Als Startpunkt der Regressionsgerade wählen Sie einen dominanten Hochpunkt oder Tiefpunkt, allerdings sollte der Trend schon vor diesem Extrempunkt eine Weile vorherrschen. Die Regressionsgerade haben stets einen möglichst kleinen Abstand zu jedem der Datenpunkte. Daher wird über den Logarithmus des Kurses der jeweilige Mittelwert im Streudiagramm durch das kleinste Quadrat ermittelt.
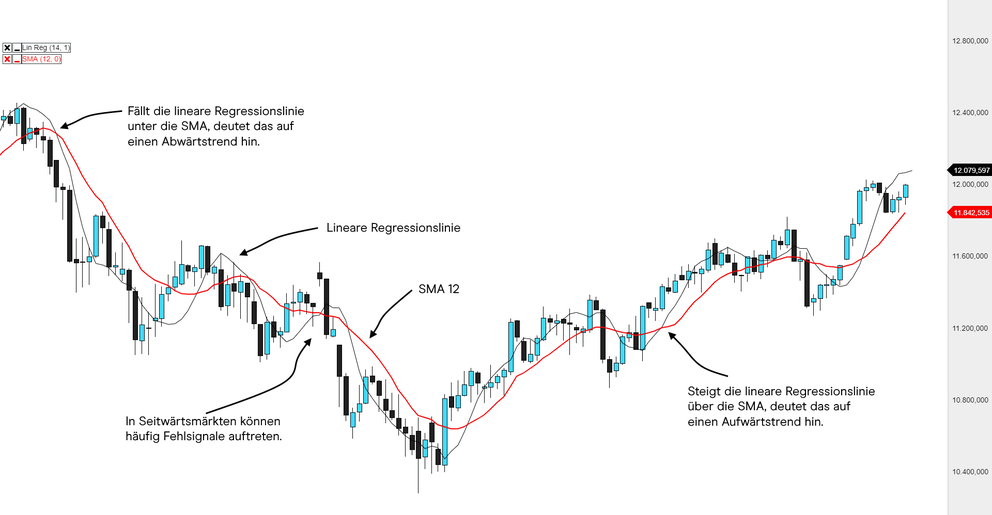
Ein Nachteil der Linearen Regression ist die Neigung zu Fehlsignalen in Seitwärtsmärkten. Dies kann bis zu einem gewissen Grad umgangen werden, indem man sie in Verbindung mit einem Stochastik-Indikator nutzt. Außerdem kann die Regressionsanalyse lediglich bei Kursverläufen mit einem stabilen vorherrschenden Trend effektiv angewandt werden und ermöglicht keine Prognose von Trendumschwüngen.
Trotzdem ist die Lineare Regression ein einfach zu bestimmender und zuverlässiger Indikator für die Technische Analyse, um einen Trend in stark tendierenden Märkten zu bestimmen. Die geringe Verzögerung der Kursbewegungen machen diese Methode besonders attraktiv.
Von der Regressionsgeraden kann auch ein Regressionskanal, der sogenannte Raff-Channel, abgeleitet werden. Dazu wird das Regressionsmodell parallel einmal nach oben und einmal nach unten an den jeweiligen Höchstkurs bzw. Tiefstkurs verschoben, sodass der Trendkanal den gesamten Kursverlauf umschließt.
Obwohl die Lineare Regression wie ein SMA aussieht, reagiert sie weitaus sensibelauf Marktveränderungen. Sie kann auch genutzt werden, um anhand der Preise während der betrachteten Periode Aussagen über die Preisentwicklung in der nächsten Periode zu treffen.
Die Lineare Regression kann verschieden angewandt werden, am gebräuchlichsten ist die Verwendung in Verbindung mit einem gleitenden Durchschnitt, beispielsweise einem SMA, wie in der Abbildung gezeigt. Schneiden sich beide Linien, wird ein Kauf- oder Verkaufssignal generiert.

Kostenloses Demo-Konto
Testen Sie CFD-Trading risikofrei, ohne Einzahlung und mit 10.000 € virtuellem Startkapital.