Fibonacci

Fibonacci ist eine Methode, um den Korrekturbereich (potentielle Unterstützungs- und Widerstandszonen) eines Basiswertes zu finden. Seinen Ursprung hat das Fibonacci-Retracement in der Fibonacci-Folge nach dem italienischen Mathematiker und Finanzgenie Leonardo Fibonacci de Pisa, auch genannt Fibonacci, der dieses mathematische Phänomen im 13. Jahrhundert entdeckte.

Diese unendliche Folge ergibt sich, indem mit zwei Einsen gestartet wird und jede Zahl mit der vorhergehenden Zahl addiert wird. Durch diese Summe ergeben sich jeweils die Fibonacci-Zahlen. Heutzutage wird der Anschaulichkeit halber meistens noch eine Null vorangesetzt.

0, 1, 1, 2, 3, 5, 8, 13, 21, …

Er veranschaulichte diese Zahlenfolge an einem Kaninchenpaar. Die Simulation setzt voraus, dass jedes Kaninchen ewig lebt und im Alter von zwei Monaten fortpflanzungsfähig ist. Außerdem wird jedes der Kaninchenpaare von da an alle zwei Monate ein neues Kaninchenpaar zur Welt bringen. So steigt die Kaninchenpopulation bis ins Unendliche.

Wenn Sie nun den Quotienten zweier aufeinander folgender Zahlen berechnen, erhalten Sie immer das gleiche Verhältnis, PHI‘=0,618, was der Kehrwert der berühmten Zahl Phi ist. So ergibt sich auch schon der erste Prozentsatz oder „Ratio“ für eine Fibonacci-Linie, nämlich bei 61,8 %. Dies wird auch der goldene Schnitt genannt und Sie finden ihn auch in der Natur, beispielsweise bei Sonnenblumen, in der Kunst wie in Leonardo Da Vincis Mona Lisa und in der Architektur wieder, wie es am Parthenon deutlich wird.

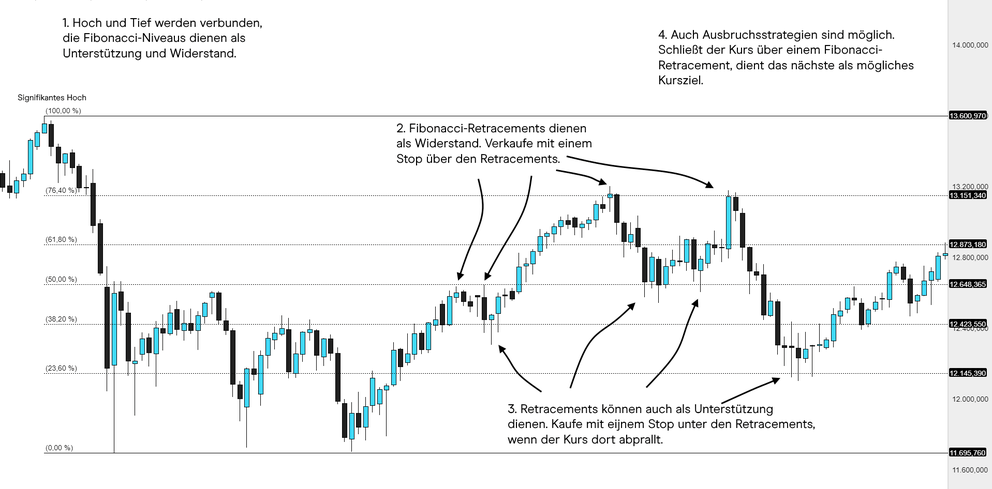
Grafisches Beispiel der Fibonacci-Methode

Die Arbeit mit dem Fibonacci-Retracement ist stark umstritten, da ihr Erfolg statistisch nicht nachweisbar ist. Trotzdem nutzen besonders Daytrader das Fibonacci-Retracement gerne, um Kurskorrekturen zu beobachten und zu prophezeien, da sich diese Methode in der Vergangenheit bewährt hat. Das Fibonacci-Retracement kann außerdem durch die Nutzung von Überkauft-Überverkauft-Indikatoren (Oszillatoren) bestätigt werden, beispielsweise durch den Williams %R (Williams Prozent Range).

Das Fibonacci-Zeichenwerkzeug umfasst die klassischen Prozentsätze von 23,6%, 38,2% und 61,8%, die durch horizontale Linien dargestellt werden. Außerdem wird eine 50%-Retracement-Linie angezeigt, obwohl es sich hierbei nicht um eine echte Fibonacci-Linie handelt, da dies keine Fibonacci-Zahl ist. Da festgestellt wurde, dass auch an der 50%-Marke sehr häufig ein entscheidender Wendepunkt vorliegt, wird sie trotzdem als ein wesentlicher Teil der Fibonacci-Analyse betrachtet und wird ebenfalls genutzt, um die Wahrscheinlichkeit einer Trendfortsetzung zu bestimmen.

Auf der vertikalen y-Achse werden die Prozentsätze abgebildet. Die horizontale x-Achse stellt die Zeit dar. Bei einem Abwärtstrend befindet sich die 0%-Marke unten, bei einem Aufwärtstrend oben.

Eine Fibonacci-Linie kann entweder als Widerstandszone, „resistance level“, oder als Unterstützungszone, „support level“, agieren. Dies bedeutet, dass sich der Kurs größtenteils innerhalb dieses Bereichs bewegen wird. Wenn der Kurs zu stark sinkt oder steigt, wird diese Entwicklung an der nächstgelegenen Fibonacci-Linie vermutlich entschleunigt, pausiert oder sogar gestoppt.

Falls eine Fibonacci-Linie doch durchbrochen werden sollte, fängt das nächste Fibonacci-Retracement die Kursbewegung auf. Ein vorherbestimmter Anteil prallt von der Fibonacci-Linie ab und wird zurückgegeben. Wenn die Korrektur dabei nur bis zur 38,2% Linie geht, wird nicht mit einer Trendwendegerechnet, sondern mit einer zeitversetzten Fortsetzung der Trend-Bewegung. Als Faustregel lässt sich darüber hinaus sagen, dass die maximale Korrektur die 61,8%-Linie nicht überschreiten sollte.

Die Trendlinie lässt sich ebenfalls mithilfe der Fibonacci-Retracements bestimmen. Für die Berechnung der Trendlinie teilen Sie die vertikale Differenz des Hoch- und Tiefpunktes durch die Fibonacci-Ratio. Auch hier finden Sie den goldenen Schnitt wieder.

Weiterführende Informationen zu den Fibonacci-Retracements und anderen Tools in der technischen Analyse finden Sie in den kostenlosen Videos unserer Privathändlerausbildung.